上次那个逻辑回归讲的很好,这次还是这个人的博客,讲了线性回归,分为梯度下降,和normal equation两部分:
第一部分,Gradient Descent方法
(一)h函数

一般表示格式按如下约定,第i条样本的输入x(i):
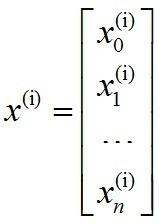
所有训练样本的输入表示为x,输出表示为y:
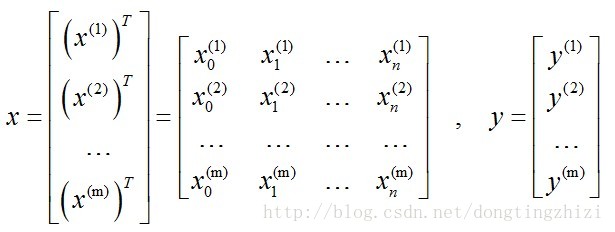
为了公式表示方便,将x0设定为1,同时将所有θ表示成向量:
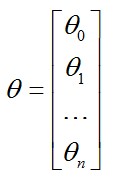
则有:

(二)J函数
linear regression中一般将J函数取成如下形式:

至于为什么取成该式,这里不进行深入的分析和推导,网上有一篇文章《Standford机器学习+线性回归CostFunction和Normal+equation的推导》进行了推导,可供参考。
向量化后简化为:

(三)gradient descent
θ的迭代公式为:

向量化后简化为:

(四)其他问题
1. Feature scaling
Feature scaling可以通俗的解释为:将不同特征的取值转换到差不多的范围内。因为不同特征的取值有可能有很大的差别(几个数量级),例如下图中的x1和x2差别就非常大。这样会带来什么后果呢?从左图中可以看出,θ1-θ2的图形会是非常狭长的椭圆形,这样非常不利于梯度下降(θ1方向会非常“敏感”,或者说来回“震荡”)。进行scaling处理后,不同特征的规模相似,因此右图中的θ1-θ2图形会近似为圆形,这样更加适合梯度下降算法。
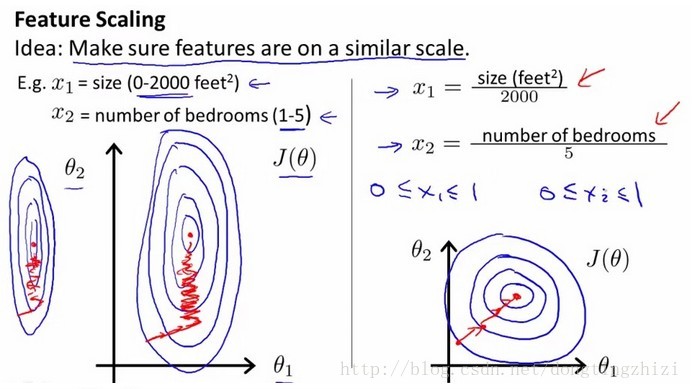
里面提到的标准差 Standard Deviation,又叫作均方差。
标准差定义是总体各单位标准值与其平均数离差平方的算术平均数的平方根。
2. vectorization
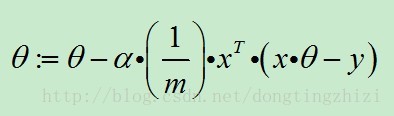
这样,不需要for循环,使用矩阵计算可以一次更新θ矩阵。
3. 关于学习率α

下图是递归下降失败的情况,J(θ)未能随每次迭代顺利下降,说明α太大,当α充分小时,每一步迭代J(θ)都会下降的。所以,此时可以尝试减小α。

但是,当α过于小时,J(θ)会下降的非常缓慢,因此需要迭代更多次数才能达到效果,浪费计算资源。所以要选择合适的α值,太大太小都不合适。一般在训练样本时,多次尝试不同的α值,对比结果(可以绘制出J(θ)迭代的图形)后进行选择。Andrew Ng老师在课程中也给出了α尝试的方法:先选择一个较小的α值,收敛太慢的话以3倍来增加α值。

第二部分,Normal equation方法
因为gradient descent方法需要迭代很多次是的J(θ)达到最小值求得θ,自然而然的会有一种疑问:能不能不迭代,一次求得所需的θ呢?答案是肯定的,normal equation就是这样一种方法。
关于normal equation,Andrew ng老师的课程中介绍的非常简单,几乎是直接给出了下面的公式。《机器学习实战》中也没有讲具体的推导,也是给出了该公式(P138页)。但是,二者都提到一个基本的数学原理,那就是当J(θ)对所有θj的偏导等于0时,J(θ)取最小值(高等数学中有当导数等于0时函数达到极值)。
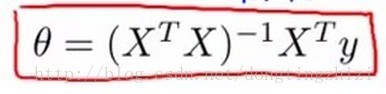
《机器学习实战》中(P138页)提到对矩阵(y-Xw)T(y-Xw)求导,得到XT(y-Xw),令其等于零可以解得上面的公式,这里我真心没有明白,求高手解释。
(1)关于non-invertibility

两种可能的解决方法:1.如果存在冗余的特征(冗余特征间存在线性依赖),去掉冗余特征;2.特征数量太大(m<=n,即样本数小于特征数),应该去掉一些特征或者使用regularization。regularization是一种消除overfitting的方法,Andrew ng老师的课程中有详细的介绍,使用了regularization的normal equation方法就不存在non-invertibility的问题了,貌似就是《机器学习实战》中介绍的局部加权线性规划方法。
总结
